Research: Applied Math
Approximation of Viscosity Solutions
Current team:
UNCG Faculty: Thomas Lewis
Graduate Students: Aaron Rapp
Other Recent Collaborators:
Xiaobing Feng (University of Tennessee)
Chiu-Yen Kao (Claremont McKenna College)
The main goal of the research is to directly approximate the viscosity solution of second order Dirichlet boundary value problems with underlying PDE
| \begin{alignat}{2} \label{problem} F[u](x) \equiv F \left( D^2 u(x), \nabla u(x), u(x), x \right) & = 0, && \qquad x \in \Omega \subset \mathbb{R}^d, \ \ \ \ \ \ (1) \end{alignat} |
where $$F$$ is an elliptic operator that is allowed to be nonlinear in the Hessian $$D^2 u$$ and $$\Omega$$ is an open, bounded domain. We have developed both a finite difference (FD) framework and a discontinuous Galerkin (DG) framework. For applications, we are mainly concerned with the Monge-Ampère equation and the Hamilton-Jacobi-Bellman equation. These equations arise in stochastic optimal control and optimal mass transport.
The key theoretical results of my research for approximating fully nonlinear equations rely upon an abstract FD convergence theory for (1) that my collaborators and I developed for one-dimensional problems and are now extending to higher dimensional problems. The theory guarantees locally uniform convergence to the viscosity solution of (1) when using FD methods that satisfy certain properties including admissibility, stability, consistency, and generalized monotonicity. In many ways, the theory is an extension of the successful FD framework of Crandall and Lions for fully nonlinear first order equations. Furthermore, the proposed framework is meant to complement the well-known framework of Barles and Souganidis by proposing alternative sufficient conditions that are based on the higher-order terms used in the discretization of the PDE operator instead of relying upon monotonicity with respect to the grid function itself.
The key component of the convergence theory is the introduction and use of the concept of a numerical operator, often denoted by $$\widehat{F}$$, that is consistent with the PDE operator $$F$$ and satisfies a monotonicity property that mirrors the elliptic structure of $$F$$. Viscosity solutions are merely bounded functions in general by their definition, so they do not have either classical or weak derivatives. To characterize such non-smooth functions using ‘derivative’ information, we only can compute and utilize their one-sided (approximate) derivatives. Thus, a numerical operator is multi-valued in the Hessian and gradient terms as a means to better capture the behavior of low regularity functions.
Given a consistent, generalized monotone numerical operator, our FD methods are defined by finding a grid function $U$ defined on a mesh $$\mathcal{T}_h$$ for the domain $$\Omega$$ such that
| $$\widehat{F} \bigl( D_\alpha^{+ +} U , D_\alpha^{+ -} U , D_\alpha^{- +} U , D_\alpha^{- -} U , \nabla_\alpha^+ U , \nabla_\alpha^- U_\alpha, U_\alpha , x_\alpha \bigr) = 0, \qquad \forall x_\alpha \in \mathcal{T}_h, \ \ \ \ (2)$$ |
where $$D_\alpha^{\mu \nu}$$ denotes a ‘sided’ discrete Hessian approximation and $$\nabla_\alpha^\pm$$ denotes a ‘sided’ discrete gradient approximation based on the standard forward/backward difference quotient operator at the node $$x_\alpha$$. Generalized monotonicity ensures $$\widehat{F}$$ is monotone with respect to various arguments: $$\widehat{F}(\uparrow,\downarrow,\downarrow,\uparrow, \downarrow, \uparrow, \uparrow, \cdot)$$. The key to designing such methods is the introduction of numerical moments. For particular choices of numerical moments in our Lax-Friedrich’s-like numerical operators, our FD framework can be regarded as a direct method that encapsulates the essence of the vanishing moment method of Feng and Neilan for indirectly approximating (1). Extensive, uniformly positive 1-D and 2-D numerical tests have been performed that support the convergence theory and show great promise for our FD framework.
After developing a convergence theory under the FD framework, we worked on exploiting the
theory using a DG framework, Nonstandard LDG methods IP-DG methods have been proposed. The idea for designing the DG framework is to build the correct derivative operators that extend the FD forward and backward difference quotient operators, and then using the derivative operators inside a numerical operator directly borrowed from the FD framework. To account for the finite dimensional DG basis, the numerical operator is simply projected into the DG space. We have built a DG scheme that is equivalent to the convergent FD method defined by (2) when using piecewise constant basis functions on a uniform rectangular grid. Thus, we inherit the convergence of the FD method when using piecewise constant functions, and, for higher degree basis functions, we heuristically expect to achieve increased accuracy. The use of a numerical operator is especially important due to the lack of a traditional variational formulation caused by the nonlinearity and the entirely local ‘differentiation by parts’ characterization of viscosity solutions.
Another direction of research is the application of the framework for first order fully nonlinear problems (also called Hamilton-Jacobi problems). By using numerical moments, higher-order methods are proved to converge to the underlying viscosity solution. Thus, the methods overcome the first-order accuracy barrier of monotone methods.
Definition. A function $$u\in C(\Omega)$$ is called a viscosity subsolution (resp. supersolution) of (1) if, for all $$\varphi\in C^2(\overline{\Omega})$$, if $$u-\varphi$$ has a local maximum (resp. minimum) at $$x_0\in \overline{\Omega}$$, then we have $$F(D^2\varphi(x_0),\nabla \varphi(x_0), u(x_0), x_0) \leq 0$$ (resp. $$F(D^2\varphi(x_0),\nabla \varphi(x_0), u(x_0), x_0) \geq 0$$). The function $$u$$ is said to be a viscosity solution of (1) if it is simultaneously a viscosity subsolution and a viscosity supersolution of (1). See Figure 1 for a visual representation of a viscosity subsolution and viscosity supersolution in two dimensions.
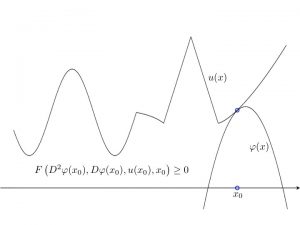 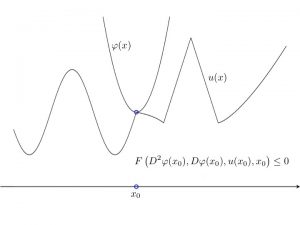 |
| Figure 1 |
Current Projects
- X. Feng and T. Lewis. Narrow-stencil finite difference methods for approximating viscosity solutions of Hamilton-Jacobi-Bellman equations.
- X. Feng and T. Lewis. Convergent finite difference methods with second order local truncation error for Hamilton-Jacobi equations.
- X. Feng and T. Lewis. Local discontinuous Galerkin methods for second order fully nonlinear elliptic and parabolic equations in high dimensions.
Related Publications
- X. Feng, T. Lewis, and M. Neilan. Discontinuous Galerkin finite element differential calculus and applications to numerical solutions of linear and nonlinear partial differential equations. J. Comput. Appl. Math., Special Issue on Recent Advances in Numerical Methods for Systems of Partial Differential Equations, Volume 299, p. 68 — 91. 2016.
- X. Feng and T. Lewis. Mixed interior penalty discontinuous Galerkin methods for fully nonlinear second order elliptic and parabolic equations in high dimensions. Numer. Methods Partial Differential Equations, Volume 30, Issue 5, p. 1538 — 1557. 2014.
- X. Feng and T. Lewis. Mixed interior penalty discontinuous Galerkin methods for one-dimensional fully nonlinear second order elliptic and parabolic equations. J. Comp. Math. Volume 32, Issue 2, p. 107 — 135. 2014.
- X. Feng and T. Lewis. Local discontinuous Galerkin methods for one-dimensional second order fully nonlinear elliptic and parabolic equations. J. Sci. Comput. Volume 59, Issue 2, p. 129 — 157. 2014.
- X. Feng, C. Kao, and T. Lewis. Convergent finite difference methods for one-dimensional fully nonlinear second order partial differential equations. J. Comput. Appl. Math. Volume 254, p. 81 — 98. 2013.





