Research: Applied Math
Discontinuous Galerkin Finite Element Methods
Current team:
UNCG Faculty: Thomas Lewis
Graduate Students: Aaron Rapp
Other Recent Collaborators:
Xiaobing Feng (University of Tennessee),
Michael Neilan (PITT),
Andreas Aristotelous (West Chester University),
Steve Wise (University of Tennessee),
Wenqiang Feng (University of Tennessee)
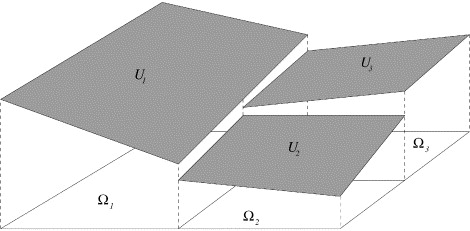
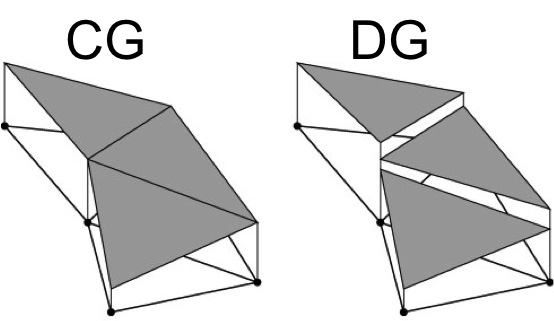
The projects focus on the design, analysis, and implementation of discontinuous Galerkin (DG) finite element methods for approximating both linear and nonlinear partial differential equations. DG methods are a generalization of finite element methods in that they allow for fully discontinuous piecewise polynomial basis functions. As such, the methods inherit the power of finite element methods while also having increased flexibility for handling problems that have inherent directions such as convection dominated processes.
The main focus of the project has been the introduction and application of the discontinuous Galerkin finite element differential calculus for approximating weak derivatives of Sobolev functions and piecewise Sobolev functions. Various discrete/numerical differential operators and their corresponding calculus rules are established based on DG methodologies. When using piecewise constant basis functions on a Cartesian partition, the DG derivatives are equivalent to well-known difference quotients from finite difference. Thus, the corresponding DG methods can be understood as high-order extensions of finite difference methods that can be posed on complex geometries. Using ideas from finite difference, new DG methods such as the (penalty free) Dual-Wind DG method can be easily formulated for both linear and nonlinear PDEs.
 |
 |
Current Projects
- X. Feng and T. Lewis. Nonstandard local discontinuous Galerkin methods for fully nonlinear second order elliptic and parabolic equations in high dimensions.
- A. Aristotelous and T. Lewis. Implementation and applications of the DWDG method.
Related Publications
- T. Lewis. Distributional derivatives and the stability of discontinuous Galerkin finite element approximation methods. Tenth MSU Conference on Differential Equations and Computational Simulations. Electron. J. Diff. Eqns., Conference 23, p. 59 — 76, 2016.
- X. Feng, T. Lewis, and M. Neilan. Discontinuous Galerkin finite element differential calculus and applications to numerical solutions of linear and nonlinear partial differential equations. J. Comput. Appl. Math., Special Issue on Recent Advances in Numerical Methods for Systems of Partial Differential Equations, Volume 299, p. 68 — 91. 2016.
- W. Feng, T. Lewis, and S. Wise. Discontinuous Galerkin derivative operators with applications to second order elliptic problems and stability. Mathematical Meth. in App. Sciences, Volume 38, Issue 18, p. 5160 — 5182. 2015.
- X. Feng and T. Lewis. Mixed interior penalty discontinuous Galerkin methods for fully nonlinear second order elliptic and parabolic equations in high dimensions. Numer. Methods Partial Differential Equations, Volume 30, Issue 5, p. 1538 — 1557. 2014.
- T. Lewis and M. Neilan. Convergence analysis of a symmetric dual-wind discontinuous Galerkin method. J. Sci. Comput. Volume 59, Issue 3, p. 602 — 625. 2014.
- X. Feng and T. Lewis. Mixed interior penalty discontinuous Galerkin methods for one-dimensional fully nonlinear second order elliptic and parabolic equations. J. Comp. Math. Volume 32, Issue 2, p. 107 — 135. 2014.
- X. Feng and T. Lewis. Local discontinuous Galerkin methods for one-dimensional second order fully nonlinear elliptic and parabolic equations. J. Sci. Comput. Volume 59, Issue 2, p. 129 — 157. 2014.





