Research: Applied Math

Reaction Diffusion Equations

Current team:

UNCG Faculty: Ratnasingham Shivaji, Maya Chhetri.
Graduate Students: Byungjae Son, Quinn Morris, Nalin Fonseka, Mohan Mallick (IIT-India).
Other Recent Collaborators:
Alfonso Castro (Harvey Mudd College), David Costa (University of Nevada Las Vegas),
R. Dhanya (Indian Statistical Institute), Pavel Drábek (University of West Bohemia),
Petr Girg (University of West Bohemia), D. D. Hai (Mississippi State University),
Eun Kyoung Lee (Pusan National University), Lakshmi Sankar (IIT-India),
Kanishka Perera (Florida Institute of Technology), Inbo Sim (University of Ulsan).

Our research interests are in steady state reaction diffusion equations and systems that arise in nonlinear heat generation, combustion theory, chemical reactor theory and population dynamics.
In particular, we are interested in existence, multiplicity, uniqueness and bifurcation results for positive steady states for various classes of reactions processes.

Figure 1: Pattern formation in fish is governed by processes which can be described using bifurcation theory	Figure 2: Reaction-diffusion equations can be used to model many problems in combustion theory.

A typical model equation in the single equation case is of the form:

Here $$\Delta_{p}u:=\mbox{div}(|\nabla u|^{p-2}\nabla u)$$ with $$p>1$$ is the $$p$$-Laplacian operator, $$\lambda>0$$ is a real constant, $$\Omega$$ is a smooth bounded domain in $$\mathbb{R}^{N}$$, and $$Bu\equiv u$$ or $$Bu\equiv\frac{\partial u}{\partial y}+c(u)u$$ where $$\frac{\partial u}{\partial y}$$ is the outward normal derivative of $$u$$ on $$\partial\Omega$$ and $$c:[0,\infty)\rightarrow(0,\infty)$$ is a continuous function.

Our current research focuses on problems of the form $$\eqref{1}$$ with continuous nonlinearities $$f:(0,\infty)\rightarrow \mathbb{R}$$ of the positone, semipositone, infinite positone, and infinite semipositone types, defined as,

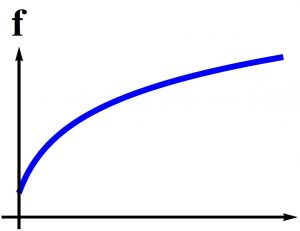
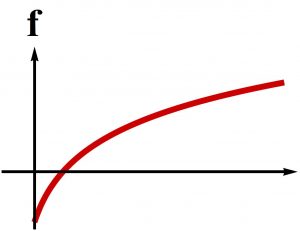
positone: $$f(0)>0$$, semipositone: $$f(0)<0$$, infinite positone: $$\lim_{s \to 0^+} f(s) = \infty$$, and infinite semipositone: $$\lim_{s \to 0^+} f(s) = – \infty$$.
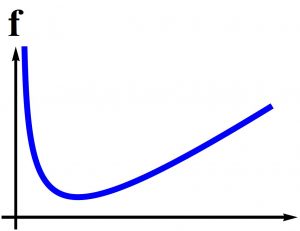Figure 3: Positone Problem	Figure 4: Infinite Positone Problem
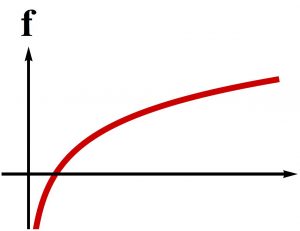Figure 5: Semipositone Problem	Figure 6: Infinite Semipositone Problem

We are also interested in the analysis of systems, including the study of combined effects of the nonlinearities.

Figure 7: PhD students Quinn Morris and Byungjae Son working on an infinite positone problem.	Figure 8: Ph.D. graduate Abraham Abebe receives his diploma from his advisor, Professor Maya Chhetri.

Recent Selected Publications

1. A uniqueness result for a semipositone $$p$$-Laplacian problem on the exterior of a ball, R. Shivaji, Imbo Sim, and Byungjae Son, accepted for publication, J. Math. Anal. Appl.
2. Existence of positive radial solutions for a superlinear semipositone $$p$$-Laplacian problem on the exterior of a ball, Q. Morris, R. Shivaji, and I. Sim, accepted for publication, Proc. Royal Soc. Edin. Sect. A.
3. On radial solutions for singular combined superlinear elliptic systems on annular domains, D. D. Hai and R. Shivaji, accepted for publication, J. Math.\ Anal.\ Appl.
4. Analysis of positive solutions for classes of quasilinear singular problems on exterior domains, M. Chhetri, P. Drabek, and R. Shivaji, accepted for publication, Advances in Nonlinear Analysis.
5. Bifurcation and multiplicity results for classes of $$p,q$$-Laplacian systems, R. Shivaji and B. Son, accepted for publication, Topological Methods in Nonlinear Analysis.
6. Positive radial solutions to classes of singular problems on the exterior domain of a ball, Eun Kyoung Lee, R. Shivaji, and Byungjae Son, J. Math.\ Anal.\ Appl., Vol.\ 434, 2016, No.\ 2, pp.\ 1597–1611.
7. Global bifurcation of positive solutions for a class of superlinear elliptic systems, M. Chhetri and P. Girg, J. Differential Equations, Vol. 261, 2016, No. 10, 5719–-5733.
8. Existence of positive radial solutions for superlinear semipositone problems on the exterior of a ball, R. Dhanya, Q. Morris, and R. Shivaji, J. Math.\ Anal.\ Appl., Vol.\ 434, 2016, No.\ 2, pp.\ 1533–1548.
9. Asymptotically linear system of three equations, M. Chhetri and P. Girg, J. Differential Equations, Vol. 261, 2016, No. 10, 5900–-5922.
10. On the solvability of asymptotically linear systems at resonance, M. Chhetri and P. Girg, J. Math. Anal. Appl., Vol. 442, 2016, No. 2, 583–-599
11. Existence of positive solutions for a class of $$p$$-Laplacian superlinear semipositone problems, M. Chhetri, P. Drabek, and R. Shivaji, Proc.\ Royal Soc.\ Edin., Vol.\ 145, 2015, No.\ 5, pp.\ 925–936.
12. Uniqueness of positive radial solutions for a class of semipositone problems on the exterior of a ball, Eunkyung Ko, Mythily Ramaswamy, and R. Shivaji, J. Math.\ Anal.\ Appl., Vol.\ 423, 2015, No.\ 1, pp.\ 399–409.
13. A three solution theorem for singular nonlinear elliptic boundary value problems, R. Dhanya, Eunkyung Ko, and R. Shivaji, J. Math.\ Anal.\ Appl., Vol.\ 424, 2015, No.\ 1, pp.\ 598–612.
14. Positive solutions for a class of superlinear semipositone systems on exterior domains, A. Abebe, M. Chhetri, L. Sankar, and R. Shivaji, Boundary Value Problems, Article ID 2014-198, 2014, 9 pages.
15. Asymptotically linear system at and near resonance, M. Chhetri and Petr Girg, Bound. Value Probl., 2014, 2014:242.\
16. Principal eigenvalue of p-Laplacian operator in exterior domain, M. Chhetri and Pavel Drabek, Results Math., Vol. 66, 2014, 461–468.
17. Uniqueness of positive solutions for a singular nonlinear eigenvalue problem when a parameter is large, Eun Kyoung Lee, Eunkyung Ko, R. Shivaji and Byungjae Son, Bulletin Belgium Mathematical Society, Vol.\ 21, 2014 No.\ 1, pp.\ 179–184.
18. Multiplicity and uniqueness of positive solutions for elliptic equations with nonlinear boundary conditions arising in a theory of thermal explosion, Peter Gordon, Eunkyung Ko and R. Shivaji, J. Nonlinear Analysis Series B: Real World Applications, Vol.\ 15, 2014, pp.\ 51–57.
19. Positive solutions for a class of superlinear semipositone systems on exterior domains, Abraham Abebe, M. Chhetri, Lakshmi Sankar and R. Shivaji, Bound. Value Probl., 2014, 2014:198.