Research: Number Theory
Well-rounded forms and the Voronoi tessellation
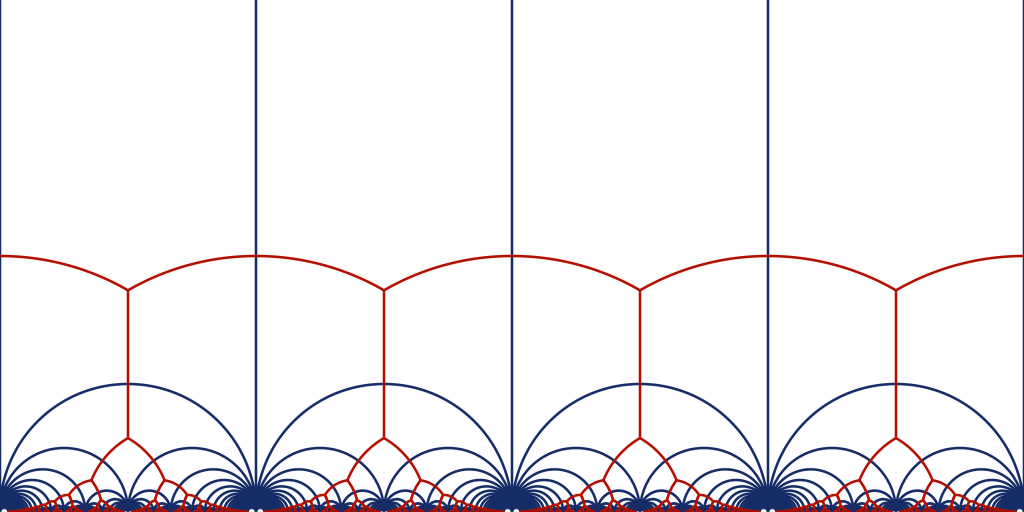
One identifies the space of binary quadratic forms with the upper half plane $$\mathfrak{h}$$. The set of well-rounded forms corresponds to an infinite tree (red). The vertices of this tree correspond to perfect forms, and dualizing gives the Voronoi tessellation of h by hyperbolic triangles (blue). This structure can be used in the study of modular forms. In joint work with F. Hajir and P. Gunnells, D. Yasaki studied a 7-dimensional analogue of this structure in the investigation of cusp forms over a CM quartic field in Modular forms and elliptic curves over the field of fifth roots of unity.





